1. Propriétés des opérations

    2. Identités remarquables

    3. Fractions

    4. Puissances

    5. Racines carrés et racines n-ièmes

    6. Polynômes

    7. Méthodes de factorisation

    8. Résolution d'équations

Définitions : Un monôme d'une variable réelle est une expression de la forme `a*x^n`, où a est le coefficient (`in RR`), x est la variable (`in RR`) et n est le degré (`in NN`).

                     Un polynôme d'une variable réelle est une somme de monômes de cette variable. C'est donc une expression de la forme

`p(x)=a_n*x^n+a_(n-1)*x^(n-1)+...+a_1*x+a_0`,

                     où les `a_i` `(0<=i<=n)` sont les coefficients (`in RR`) avec `a_n !=0`, x est la variable (`in RR`) et n est le degré (`in NN`).

Cas particuliers : Un binôme du 1er degré est un expression de la forme `a*x+b`, où a et b sont les coefficients avec `a != 0` et x est la variable.

                              Un trinôme du 2e degré est une expression de la forme `a*x^2+b*x+c`, où a, b et c sont les coefficients avec `a != 0` et x est la variable.

Définition : Le degré d'un polynôme `p(x)` est l'exposant le plus élevé de la variable. On le note : `d°(p(x))`.

Egalité de deux polynômes : Deux polynômes `p(x)=a_n*x^n+a_(n-1)*x^(n-1)+...+a_1*x+a_0` et `q(x)=b_m*x^m+b_(m-1)*x^(m-1)+...+b_1*x+b_0` sont égaux

                                                si et seulement si ils ont le même degré, c.-à-d. `m=n` et les mêmes coefficients pour les termes de même degré, c.-à-d. `a_i=b_i`, pour tout `i in {0,1,2,...,n}.

                                                C'est aussi la condition nécessaire et suffisante pour que l'on ait `p(x)=q(x)`, pour tout `x in RR`.

Degré d'une somme / différence : `d°(p(x)+-q(x))<=max[d°(p(x)),d°(q(x))]`

Degré d'un produit : `d°(p(x)*q(x))=d°(p(x))+d°(q(x))`

Division euclidienne : Quels que soit les polynômes `a(x)` (dividende) et `b(x)!=0` (diviseur), il existe deux polynômes uniques `q(x)` (quotient) et `r(x)` (reste) tels que :

`a(x)=b(x)*q(x)+r(x)`, avec `r(x)=0` ou `d°(r(x))<d°(b(x))`

Lorsque `r(x)=0`, on dit que la division est exacte et que `q(x)` est le quotient exact de `a(x)` par `b(x)`.

Exemples :

a) Schéma de la division euclidienne : Effectuons la division euclidienne de `2x^3+3x-1` par `x^2-2x+3` :

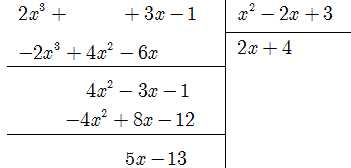
Par conséquent : `2x^3+3x-1=(x^2-2x+3)*(2x+4)+5x-13

b) Schéma de Horner : Ce schéma s'applique lorsque le diviseur est un binôme du type `x-a`, où `a` est une constante.

Effectuons par exemple la division euclidienne de `x^3-3x+4` par `x+2` :

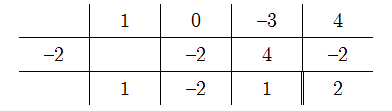
Par conséquent : `x^3-3x+4=(x+2)*(x^2-2x+1)+2`.

La propriété suivante (loi du reste) montre que le schéma de Horner s'applique également pour évaluer un polynôme en un réel..

Dans l'exemple précédent, on a : `x=-2 => x^3-3x+4=2`.

Loi du reste : Dans la division euclidienne d'un polynôme `p(x)` par un binôme de la forme `x-a`, le reste est constant et vaut `p(a)`.

Corollaire : Le polynôme  `p(x)` est divisible par `x-a` si et seulement si `p(a)=0`.

Définition : Une racine ou zéro d'un polynôme est un réel `a` tel que `p(a)=0`.

                    Si `p(x)=(x-a)*q(x)` et `q(a)!=0` alors `a` est appelé une racine simple de `p(x)`.

                    Si `p(x)=(x-a)^2*q(x)` et `q(a)!=0` alors `a` est appelé une racine double de `p(x)`.

                    En général : Si `p(x)=(x-a)^n*q(x)` et `q(a)!=0` alors `n` est appelé l'ordre de multiplicité de la racine `a` de `p(x)`.

Représentation graphique d'un polynôme : voir  Analyse/Fonctions usuelles.